Introduction:

The basic equation d (distance) = s (speed) x t (time) works to measure how far you've carried a football, the distance from Earth to another galaxy, and everything in between. When the distance is very great or very small, differences in the accuracy of our standards and the methods we use make a lot more difference.

Where you are on Earth is defined by your horizontal coordinates (latitude and longitude) and your elevation. When we use GPS, this information is provided by a system of 30 satellites. Four of these satellites are always visible from any point on Earth. They are in contact with a network of ground monitoring stations around the world and GPS receivers known as Continuously Operating GPS Reference Stations (CORS).

Your GPS receiver computes the distance to the satellites based on the amount of time it takes for a radio signal to pass between the satellite and the receiver. The system is calibrated by signals between the satellite and ground reference stations. The signal travels at the speed of light - one of the constants on which our measurement system is based. The satellite contains an atomic clock that's more accurate than the one in the receiver. At set intervals, the satellite communicates with ground stations to check location. The satellite signal appears to begin later than the signal generated by the receiver because of the time required for the signal to travel from the satellite to the receiver. This time delay is proportional to the distance between the satellite and the receiver. So the difference in time tells us how far the satellite is from the station and your device. The clocks in the satellite are accurate to three nanoseconds, which is three-billionths of a second. Tomorrow's atomic clock may be accurate to 18 significant figures.

The Master Clock at the Naval Observatory (one of two in the nation) has an accuracy of 10 nanoseconds (10 one-billionths of a second). In the GPS system, that corresponds to a position accuracy of 10 feet.

Discuss:

1. Where do the directions come from for your automobile's GPS?Local municipalities provide them.
2. What determines the accuracy of GPS directions?They can only be as accurate as the agencies that provide them. In some cases, USGS satellites are involved in creating maps. But there are some areas (mainly rural) where the information is incomplete.
3. Does GPS accuracy depend on your location on Earth?In general, satellites cover all of the Earth. Rural areas might have incomplete mapping information.
4. What could cause your GPS to provide inaccurate directions?In addition to the geographical information that is provided, the clocks must be very accurate.

Materials:

• Supporting Material - Map of Africa Be careful as you print out the PDF map of Africa. Some printers have a "fit to page" option that changes the size. Printing the map in actual size is essential for the circles to intersect.
• Local map
• GPS receiver
• Ruler
• Compass

Safety Notes:

There are no anticipated safety risks associated with this activity.

Procedure:

Read more about GPS at Web Link - How Does GPS Work? Depending upon the student's background, you may wish to read and discuss the NASA article first.

Today's GPS applications are very user-friendly; you can simply talk to your device's avatar and find out exactly where you are and how you are moving. But only two decades ago, users had to use the raw data from the satellite and calculate the time of the signal to determine their location mathematically.

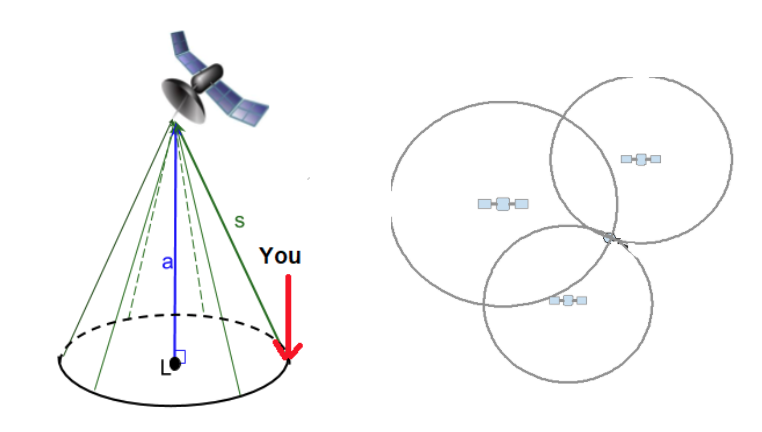
Your challenge is to determine the location of a modern-day JASON Argonaut who is traveling in Africa. Your guiding stars are 4 of the 30 satellites in the Global Positioning System. You will take the information provided from three satellites and determine the location of the Argonaut in Africa using trilateration. The 4th satellite would give you your altitude, but we will not consider that here.

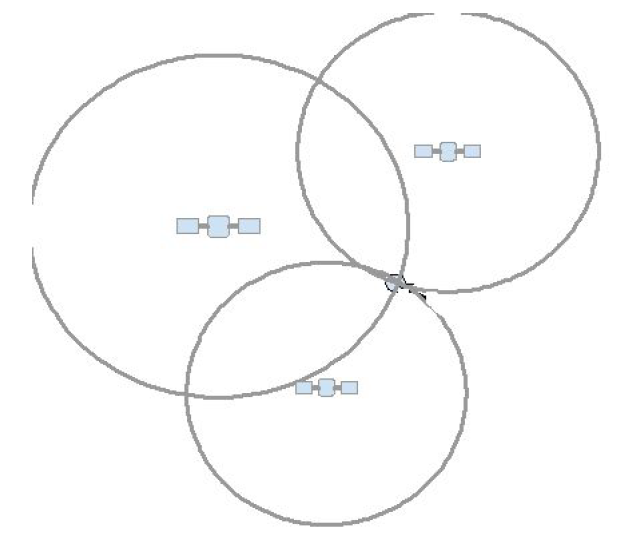
Figure 1:  Each satellite generates a circle of likely locations. The point where the circles from three different satellites intersect identifies your location on Earth.  

Satellite information:

The table below contains the data received from the three satellites receiving a signal from the Argonaut's GPS.

Helpful information:

• Every satellite constantly beams out signals that are time-stamped records of its position (a) at that time.
• The signals are carried by radio waves that travel at the speed of light (c = 299,792,458 meters per second). 
• d (distance) = c (speed) x t (time),  note that in this case d = s
• Pythagorean Theorem:  a² + r² = s²

Open the map and use it during the rest of the activity: Supporting Material - Map of Africa

To determine the location on the map, you must know the radius of the circle for each set of possible locations. We'll do the first circle together, then you complete the second and third circles.

Satellite S1

Here's what you'll do:

1. Calculate the time it takes for the signal to travel between satellite and receiver and enter your value in the table. 

s can be calculated by multiplying the travel time for the signal by the speed of light

s = travel time for signal × speed of light

s = (0.0625677 sec) × (299792 km/sec) ≈ 18,757.30 km

2. Calculate the radius of the circle of possible positions using the Pythagorean theorem. 

a = 18,725 km

Pythagorean theorem will be used to determine the radius

a² + r² = s²

(18725)² + r² = (18757.30)²

350,625,625 + r2 = 351,836,303.29

r² = 351,836,303.29 - 350,625,625

r² = 1210678.29

r ≈ 1100 km

3.  Draw the circle of possible locations on the map of Africa. 

• Note that the legend on the map indicates that 1 cm = 500 km. Adjust the value of your r to match this scale. r₁ = 1100 km / 500 km...so r = 2.2 cm, r₂ = 5 cm, r₃ = 3.5 cm
• Use the location of the satellite 5°S, 20°E as the center of the circle and plot the possible positions with your compass and ruler. 

4. Repeat steps 1-3 for Satellites 2 & 3.  

JASON Argonaut's Location

1. In what country is the JASON Argonaut? Zambia
2. What are their coordinates? (25,-15) or 15°S, 25°E
    

Analysis:

1. Why is the speed of light important in the calculation of distance? It is the constant and the variable s in the equation for distance.
2. Africa moves about a centimeter farther from South America each year. How does that affect the accuracy of the system? Land-based stations must be recalibrated.
3. What other factors affect the accuracy of a GPS location? The software in the satellite and in the receiver. Teacher note: If the three circles do not intersect at a specific point, the error is insignificant figures--rounding error.
4. What is the standard for the clocks used in the system? We use the Naval Observatory Clock; the ultimate standard is the radioactive signal of Cesium.
5. If you wanted a 3-dimensional location (with altitude), what further information would you need? A fourth satellite.
6. The GPS system also uses ground stations to continually monitor and adjust information about the position of the satellites. What might make a satellite signal change? Bits decay.
7. Use the information for satellite 1. Imagine that the satellite's orbit decayed by 2 percent. What would this change of altitude mean to the GPS location? You would redo the calculation with the altitude adjusted.
8. If your three circles did not converge exactly on one point, what explanation could you give? There are significant rounding errors in this calculation. This is an ideal time to begin to talk about precision and significant figures in anticipation of Lesson 2. The comparison of the precision of your centimeter ruler and the speed of light can begin the conversation.
    

Additional Resources:

• Web Link - NOAA: Geodesy
• Web Link - GPS.gov GPS Overview