Read the article by Elizabeth J. Gentry and Georgia L. Harris.

Supporting Material - Measure for Measure - Accuracy Matters. By Elizabeth J. Gentry and Georgia L. Harris

Show your understanding by responding to these questions. 

1. The word “tolerance” is used in the first paragraph. In conversation, we talk about things we can or cannot tolerate (like mustard on your hot dog or very screechy music.) What is the meaning of the word to metrologists (measurement experts)?
   1. How much variation could you tolerate in an estimate of how long it will take you to get to an appointment?
   2. What field or product would have extremely low tolerance?
   After several students have volunteered possible answers, explain that tolerance refers to the acceptable amount of error in measurement when making a product. Tolerance is represented in parentheses after the actual value of a measurement. For example, the value "10 mm (+0.05 -0.01)" for the length of a part indicates that all parts produced must have lengths that fall between 10.05 and 8.99 mm.
2. Describe something in your everyday life that it is important to measure.
   1. What units do you measure it in?
   2. What degree of uncertainty could you tolerate in that measurement?
   The amount of decimal places in a measurement value is determined by the readability, or resolution, of the measuring instrument. A calculator can give values with many more decimal places.
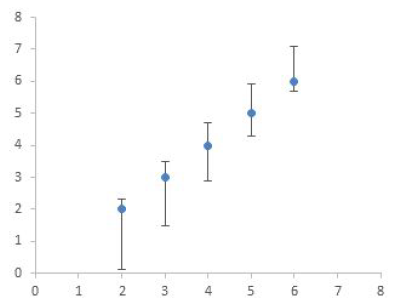
3. The graph shows a series of values with “error bars.” What do they mean? Why does knowing uncertainty in a measured value provide confidence in the measurement result?
   
   
   
   It quantifies the boundaries or limits within which a measurement result should agree with a true quantity value.
4. The text says, “It’s a wise practice to ask for the measurement uncertainty and use it to assess the quality and precision of a measurement result.” Imagine you are managing your friend’s campaign to be elected as a local representative. How would this apply?
   Students might imagine polls and their margin of error.
5. Restate the following to explain it as simply and clearly as possible: “the VIM defines “accuracy” — as it’s related to a measurement result — as the “closeness of agreement between a measured quantity value and a true quantity value of a measurand.” How is this similar to or different from the definition of accuracy we’ve used so far?
   The “true quantity” is what we have referred to as a standard (now, a constant.)
6. Give an example of a real-life “black dot” and how it might affect the people involved.
   A very visible error in any study or process can discredit it or create doubt about subsequent work. For example, when NASA confuses units, they create doubt about future missions.