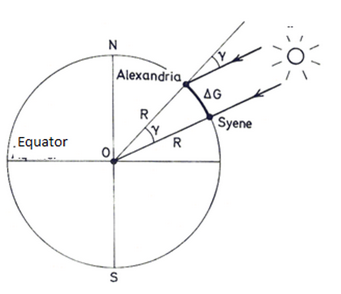
Around 240 BCE, the Greek mathematician Eratosthenes measured the angle of a shadow in Alexandria. He knew the distance to the city of Syene, where his students measured the same shadow angle. Using those figures, he was able to estimate that the circumference of the Earth was 39,250 miles (63,167 km). He was within about 2 percent of the actual value (off by about 402 meters in estimating the diameter). By contrast, if the points had been measured today with GPS, each might have been located within about 4 meters.

There’s an old saying: “Close only counts in games of horseshoes.” In science and technology, the most important question is, “How close?” Like all things STEM, these questions are answered by odds: What are the chances that this same question will be answered the same way next time and every time?

Precision involves two separate measures, reproducibility (Will your measurement be the same if someone else takes it?) and reliability (Will your measurement be the same the next time?) Without precision, people who do the same task in different places or at different times cannot be confident that they will get (essentially) the same answer.

Mini-STEM: Pointing to a Pole

While Santa may not believe it, the North Magnetic Pole actually moves around. That causes a lot of problems for birds, sea turtles, and the maintenance crews at big airports! In 2011 the FAA renumbered the main runway at the airport in Tampa, Florida. It had been designated 18R/36L, which means it was aligned along 180 degrees from north (that is, due south) when approached from the north and 360 degrees from north when approached from the south. Now the Federal Aviation Administration (FAA) has requested the designation be changed to 19R/1L. Tampa is at latitude 29..5 N. Each degree of latitude is about 110 kilometers. Estimate how far off a plane would be if it followed the old line rather than the new one.[a]

WIth these differences in mind, it’s easy to understand that precision depends on the measuring instrument and the measurer. If you are using a tape measure marked in centimeters, it’s hard to be much more precise than halfway between the marks. An electronic distance meter might have far more precise measurements. If the measurement you are taking requires several different instruments, the answer cannot be more precise than the least precise step.

While accuracy is an objective parameter (especially when constants are used for comparison), precision is relative. It depends on how much variation a given procedure can allow. Buying enough food for a party can be “more or less” precise; manufacturing a dose of a drug needs much more precision. Identifying a persistent chemical in a lake system might involve parts per million, while calculating the chances of a subatomic particle hitting a given target might require far more precision.

Mini-STEM: Bike On

A bicyclist has a GPS on her phone, and also has a physical meter on her front tire to measure distance traveled. The meter is calibrated by measuring circumference of the wheel with a tape marked in centimeters. It then counts the number of turns.

The GPS is accurate to about 4 meters. If the cyclist travels one kilometer, which instrument is most precise?[b]

But Spock Says…

Many fans of the old science-fiction series Star Trek shared a repeated “in joke” when First Officer Spock would make an estimate of the odds of something happening: “Captain, I estimate that we have a 3.45235 chance of surviving this problem.” How could he know? What instrument could really tell him that? (The implication was always that he was guessing, which Vulcans never do, and that’s why it was funny to real scientific thinkers.)

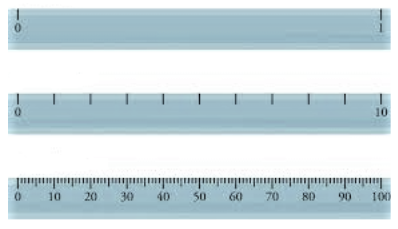
In any STEM investigation, we need to think about whether our numbers mean something in advance. Look at these three rulers. What is the most precise level of measurement that you could reasonably make with each of them?

Of course not. If one step in your procedure uses a tool that measures in centimeters, your answer can’t suggest that you know the result in micrometers no matter what the calculator says. We define our confidence in our answer in terms of significant figures.[c]

Famously Imprecise Moments in History:

A Trip to Tokyo and the Millimeter Malfunction

On December 5, 2003, twelve passengers on Space Mountain at Disneyland Tokyo were shocked when the ride derailed and came to a sudden stop. The cause of the derailment was a broken axle. The axle broke because it was the wrong size. In 1995, the specifications for Space Mountain were changed to metric units. However, for some reason, in 2002, the person who ordered the axles used the imperial unit plans from prior to 1995. Therefore, instead of ordering 45 mm axles, 44.14 mm axles were purchased instead. While this error may seem small, it was large enough to cause a malfunction.

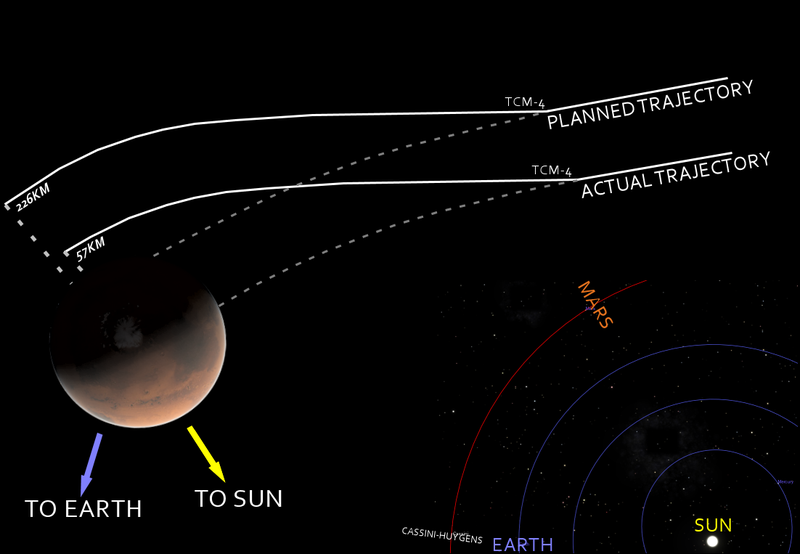
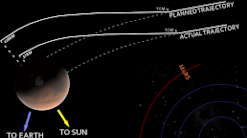
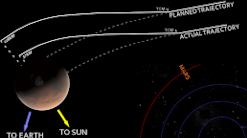
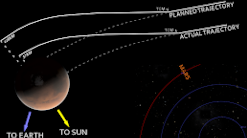
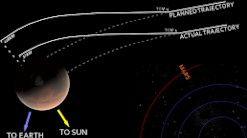
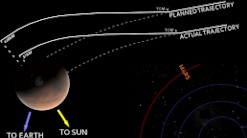
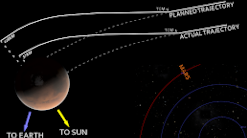
The Mission to Mars and the Multimillion Dollar Metric Miscalculation

In 1999, NASA launched Mars Climate Orbiter (MCO) which would investigate Mars’ atmosphere, climate, and surface. As the name states, MCO was intended to enter an orbit around Mars; however, MCO actually entered Mars’ atmosphere and disintegrated due to the atmospheric pressure. After a review, the cause for the error was found. The propulsion engineers expressed the necessary force for MCO’s thrusters in imperial units (pounds) while NASA’s engineers assumed the numbers were in metric units (Newtons) as was common for space missions. This simple mathematical mistake cost NASA a piece of equipment that cost $125 million.[d]

The Metric Mix-Up and the “Gimli Glider” Gaffe

In 1971, the Canadian government established Metric Commission Canada to plan and coordinate the switch measurement systems from imperial to metric. Still, the change came slowly as the government faced resistance to the change. The change caused some serious mistakes as well. In July 1983, Air Canada Flight 143 was scheduled to fly between Montreal and Edmonton; however, the plane had to land mid-flight as it was almost out of fuel. This flight was the first in which the metric system was to be used. Therefore, instead of correctly calculating the liters of fuel required for a 22,300 kg payload, the crew calculated the fuel necessary for a payload of 22,300 pounds, resulting in only having approximately half of the fuel necessary for the flight. The pilots acted quickly to land safely, gliding the last 100 km to an airport in Gimli, Canada.[e]

Arabic or Roman Miles? Columbus Misinterprets Al-Farghani

“In fourteen hundred ninety-two, Columbus sailed the ocean blue.” Had mathematical precision not been an issue for him, he may have reached his true destination. So, why did Christopher Columbus believe that he landed in India instead of his actual landing point in the Bahamas? Well, partially due to a miscalculation of Earth’s circumference. Columbus used calculations from the astronomer Abū al-ʿAbbās Aḥmad ibn Muḥammad ibn Kathīr al-Farghānī of the Abbasid court in Baghdad (also known as Alfraganus). Al-Farghani’s calculations were fairly accurate, which is particularly impressive when considering the technologies available when al-Farghani was alive in the 9th [f]century. Al-Farghani calculated that one degree latitude was the equivalent of 111.8 km, while the modern value is 111.3 km. However, al-Farghani’s calculations were in the Arabic mile (7,091 feet per mile), and Columbus assumed they were in Roman miles (4,856 feet per mile). This miscalculation alone meant that Columbus calculated Earth’s circumference to be approximate ¾[g] of its actual length. To compound the mistakes, Columbus also wrongfully assumed that Asia was much further east than it actually was. It is unclear how he determined this, however.

Mini-STEM: Around the Corner

Imagine you are an architect designing a new wing on a high school. The wing is designed to be rectangular, 80 feet by 120 feet. Your construction foreman, who has only worked in Europe, brings his metric measurement tools and measures to the nearest centimeter. But the subcontractor uses English measurements, and measures to the nearest half inch. What is the difference in the dimensions of the building by each method?

The corners of the wing are designed to be exactly 90 degrees, but the concrete subcontractor is off by .5 degree, creating a corner that is 90.5 degrees. How far off will the wing be at the opposite end of the structure?

The floor of the new wing will be covered by tiles that are 2 x 2 feet square. How many additional tiles will be needed (cut) to accommodate the construction error?[h]

Your Turn

You are in charge of a factory that makes a vital product. It could be respirators for hospitals, planting tools for farms, or gears for a jet airplane. Each machine must work the first time, every time, exactly the same way. What steps would you take to assure precision in your product?